Chapter 2: Implement the Battleship circuit in Zokrates
Design circuit
The first thing is to design the circuit for the game, which enforces the rules of the game listed as below:
-
The game board is a 10*10 grid;
-
There are five ships placed on board, either horizontally or vertically. And they should have the following size:
- Carrier: 5;
- Battleship: 4;
- Cruiser: 3;
- Submarine: 3;
- Destroyer: 2.
-
Once the fleet are placed on board before a game starts, they cannot be moved during the game;
-
A shot represented by coordinates of (x, y) should be within the board and either hits or misses a fleet.

Next we determine the inputs and outputs of the circuit.
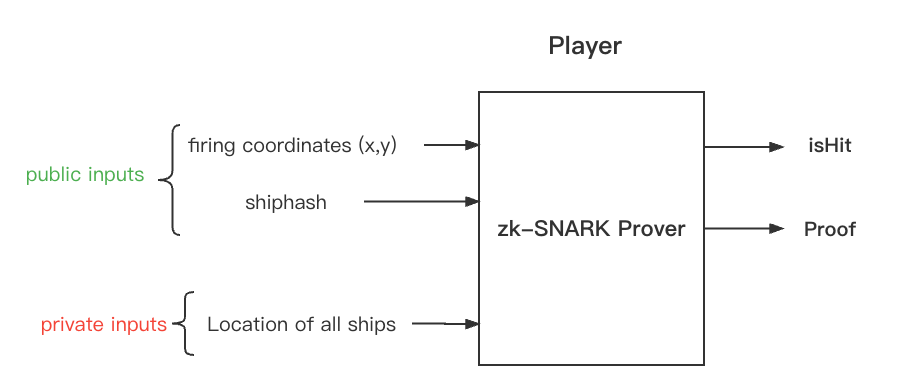
- Inputs:
- Private inputs: all the information about the fleet location
- tuples of
(pos_x, pos_y, direction)indicating each ship’s position on board;
- tuples of
- Public inputs: all the information for a firing event
- a committed hash of the fleet location;
- target coordinates
(pos_x, pos_y);
- Private inputs: all the information about the fleet location
- Outputs: hit or miss any ship
Write circuit in Zokrates
Encode Fleet State
As discussed above, we can use a tuple of (pos_x, pos_y, orientation) to indicate a ship’s location on board, but how can we represent the whole fleet’s position state?
Note that the valid value of the position is between 0 to 9 and the orientation value is just 0 or 1. So we could just encode each of them in 4 bits, and connect them all to form a number that can represent the whole tuple. For example:
shipState = shipX + shipY * (1<<4) + shipOrientation * (1<<8);
With the same idea we can represent the whole fleet’s position state in just one field:
fleetState = carrierState + battleshipState * (1<<12) + cruiserState * (1<<24) + submarineState * (1<<36) + destroyerState * (1<<48);
Mimc Hash
The next thing is to calculate the hash value of the fleet state. We choose a zkSNARK-friendly hash algorithm mimc7 to do the job due to its small size in the final circuit. There are also other hash algorithms that can be used here.
We just make sure it’s the same as the declared one in public inputs:
assert(mimc7::<91>(shipState, 0) == shipHash);
Hit or Miss
First we check whether the target position is valid:
assert(targetX >= 0 && targetX <= 9 && targetY >= 0 && targetY <= 9);
Then we can put the hit or miss logic in a help function and call it in the main:
def isShipHit(field x, field y, field o, field size, field targetX, field targetY) -> bool { return ((o == 0 && targetX == x && targetY >= y && targetY <= y + size - 1) || (o == 1 && targetY == y && targetX >= x && targetX <= x + size - 1)); }
The final circuit outputs whether any ships were hit:
return (isCarrierHit || isBattleshipHit || isCruiserHit || isSubmarineHit || isDestroyerHit);
Put it to the test
Finally we get the complete circuit code as shown on the right.
If you look carefully at the code we just accomplished, you may find that we do not check the validity of the ship’s position. That means one could cheat its opponent by giving an invalid ship location as private inputs at the beginning, thus the ship could never be hit. Can you update the circuit to prevent this from happening? Try and see the answer we provided.
Credits
In fact the circuit was created based on code from this repo, with which we made some changes.